buffon'un iğnesi

pi sayısını bir çeşit olasılık hesabıyla bulmaya yarayan yöntem. fransa'da, doğa bilimleri ve matematikle ilgilenen buffon kontu georges-louis leclerc tarafından bulunduğu için onun adıyla anılır.

olay şöyle gerçekleşiyor:

elinize çok sayıda iğne alın ve eşit aralıklarla birbirine paralel olarak çizilmiş çizgileri olan bir tahtanın üzerine iğneleri atmaya başlayın. şöyle:

görselin kaynağı

görüldüğü gibi iğnelerin çizgileri kesme durumu her iğne için farklı. kimisi hiçbir çizgiye değmiyor, kimisi ucundan ya da ortasından herhangi bir çizgiyle temas etmiş durumda. bu durumda iğnelerin çizgileri kesme olasılığı nedir diye sorsak nasıl bir cevaba ulaşırız?

yukarıdaki soruya konu olan olasılık, bir iğnenin orta noktası ile iğnenin tahta üzerindeki konumunun çizgilerle yaptığı açılara bağlıdır. tabii burada tek bir iğne olmadığından, tüm iğneler için bu olasılığın ne olduğu da merak konusu olacaktır.

iğnenin çizgilerden biriyle yaptığı açıdan bahsettik. iğne kendi etrafında 360 derece yani 1 tam tur dönebilir ve bir daire çizebilir. bu 360 derecenin her birinde de çizgiyle yaptığı açı birbirinden farklı olur. elbette iğnekendi ekseni etrafındaki bu turu atarken bazı açılarda bulunduğu sırada çizgiyi keserken bazı açılarda çizgiyle temas etmez. burada ayrıntısına girmeyeceğim birtakım trigonometri ve olasılık hesaplarıyla, integral yardımıyla iğnenin çizgiye değme olasılığı hesaplanabilir.

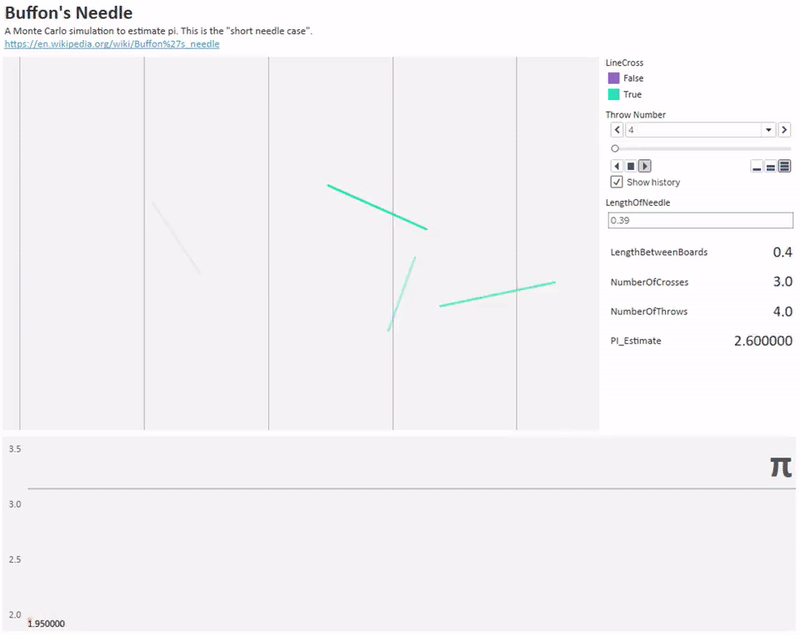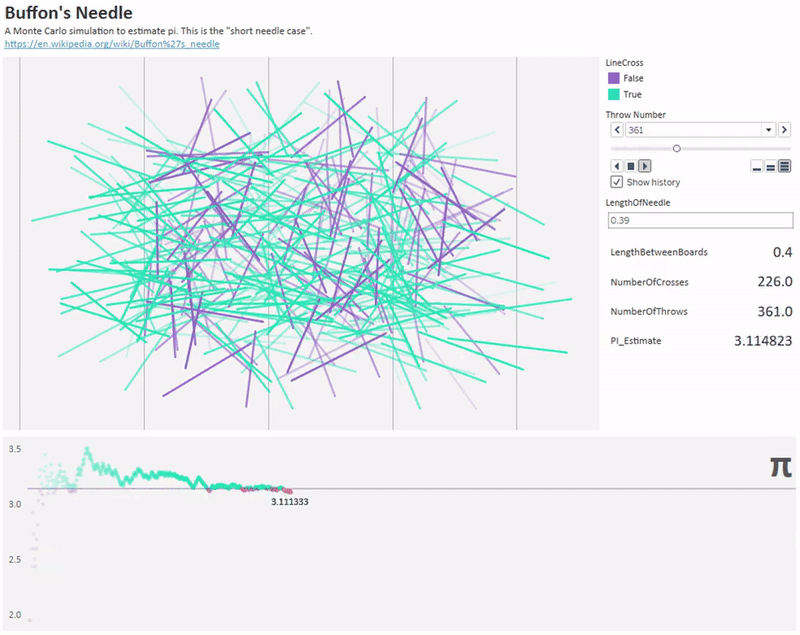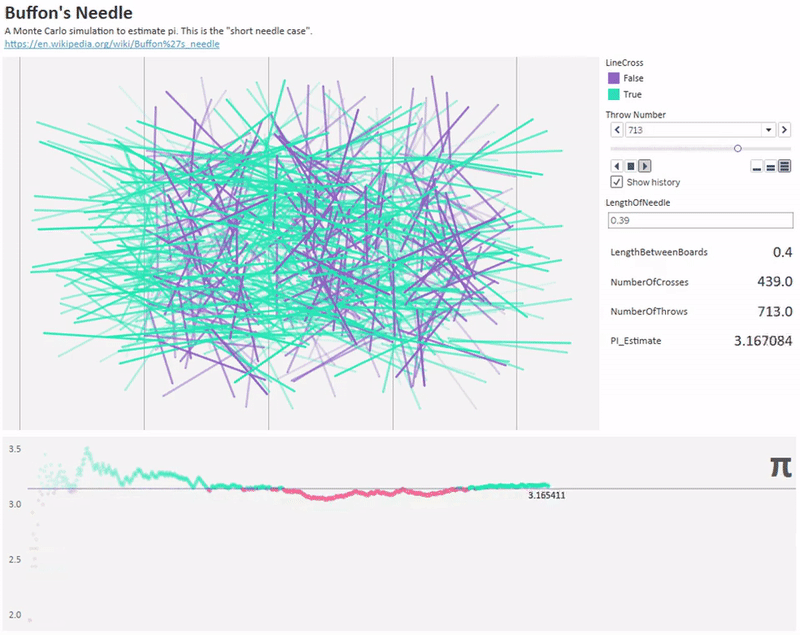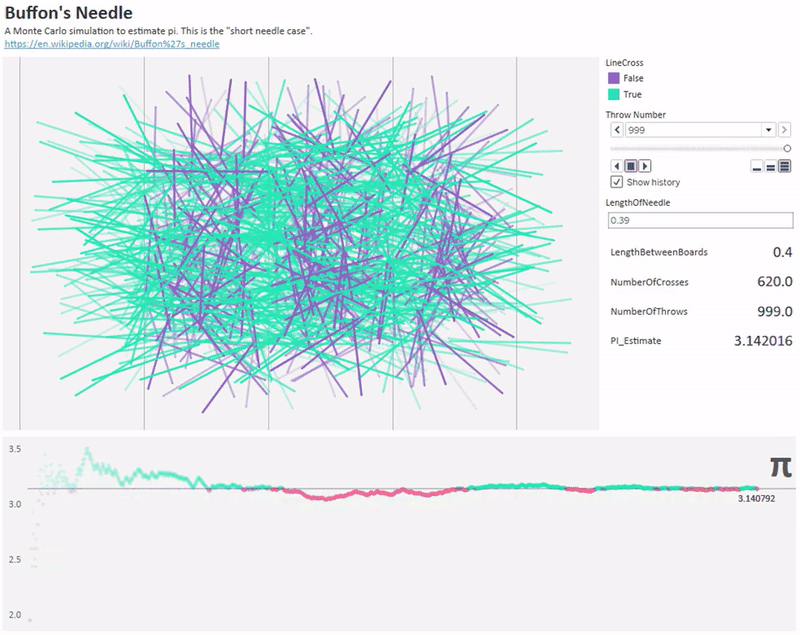
deney iğnenin uzunluğunu artırarak da yapılabilir. zira iğne 2 çizgiye birden değecek kadar uzun da olabilir. iğne sayısı arttıkça pi'ye daha yaklaşık değer elde edilebilir.

aslında yukarıdaki olasılık hesabının sonucu pi'ye bağlı olarak çıkar. ancak biz burada pi'yi bilmediğimizi ve onu hesaplamaya çalıştığımızı varsayıyoruz. bu yüzden iğneleri çok fazla kez, belki milyon defa atıp oradan çizgiye değme frekansını bulabiliriz. böylece frekanstan olasılığa geçerek ve formülden pi'yi çekerek pi'yi bulmuş oluruz. bu yönteme monte carlo metodu da denir.